Question

Rewrite in rectangular form r=8sin (theta)-2cos (theta)

Answer 1

r=8sin (Ф)-2cos (Ф)

y=sin(Ф) and x = cos(Ф) ==> r=8y -2x

Answer 2

The equation in rectangular form is:

`(x+1)^2+(y-4)^2=17`

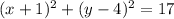
Explanation:

We are given a expression in polar coordinate form as:

`r=8\sin(\theta)-2\cos(\theta)`

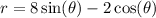
We know that:

`x=r\cos\theta\ and\ y=r\sin\theta`

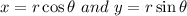
This means that:

`sin\theta=(y)/(r)\ and cos\theta=(x)/(r)`

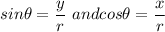
Hence,

`r=(8y)/(r)-(2x)/(r)\\\\r^2=8y-2x`

Also, we know that:

`x^2+y^2=r^2`

Hence,

`x^2+y^2=8y-2x\\\\x^2+2x+y^2-8y=0\\\\(x+1)^2+(y-4)^2=17`

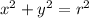
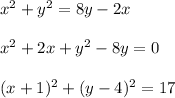
Hence, the following equation is a equation of a circle with center at (-1,4) and radius √17.