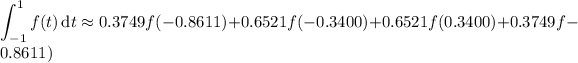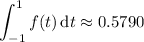Question

Apply Gaussian quadrature with n = 4 to approximate integrate sin x^2dx from 1 to 5

Answer 1

First, recall that Gaussian quadrature is based around integrating a function over the interval [-1,1], so transform the function argument accordingly to change the integral over [1,5] to an equivalent one over [-1,1].


`x=2t+3\iff t=\frac x2-\frac32\implies2\mathrm dt=\mathrm dx`

`x=1\implies t=\frac{2-6}4=-1`

`x=5\implies t=\frac{10-6}4=1`

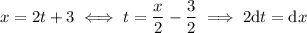
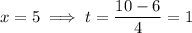
So,


`\displaystyle\int_(x=1)^(x=5)\sin x^2\,\mathrm dx=\displaystyle2\int_(t=-1)^(t=1)\sin(2t+3)^2\,\mathrm dt`

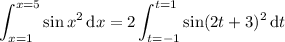
Let
`f(t)=2\sin(2t+3)^2`. With
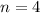
`n=4`, we're looking for coefficients
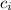
`c_i` and nodes
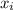
`x_i`, with
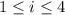
`1\le i\le4`, such that


`\displaystyle\int_(-1)^1f(t)\,\mathrm dt\approx c_1f(x_1)+\cdots+c_4f(x_4)`

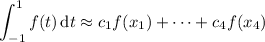
You can either try solving for each with the help of a calculator, or look up the values of the weights and nodes (they're extensively tabulated, and I'll include a link to one such reference).

Using the quadrature, we then have


`\displaystyle\int_(-1)^1f(t)\,\mathrm dt\approx0.3749f(-0.8611)+0.6521f(-0.3400)+0.6521f(0.3400)+0.3749f-0.8611)`

`\displaystyle\int_(-1)^1f(t)\,\mathrm dt\approx0.5790`