By using the equation below complete the square, write the equation of the circle in standard form from the following equation. Then determine the center and radius of a circle.…

Question

asked Oct 25, 2022 200k views

1 Answer

Orrin · Answer 1 · 2022-10-29T07:28:46+0000

Given:

The equation of a circle is

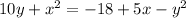
10y+x^2=-18+5x-y^2

To find:

The center and radius of the given equation by completing the square.

Solution:

The standard form of a circle is

(x-h)^2+(y-k)^2=r^2 ...(i)

where, (h,k) is center and r is radius of the circle.

We have,

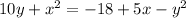
10y+x^2=-18+5x-y^2

It can be written as

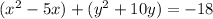
(x^2-5x)+(y^2+10y)=-18

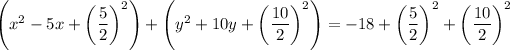
$\left(x^2-5x+\left((5)/(2)\right)^2\right)+\left(y^2+10y+\left((10)/(2)\right)^2\right)=-18+\left((5)/(2)\right)^2+\left((10)/(2)\right)^2$

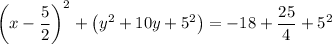
$\left(x-(5)/(2)\right)^2+\left(y^2+10y+5^2\right)=-18+(25)/(4)+5^2$

$\left(x-(5)/(2)\right)^2+(y+5)^2=-18+(25)/(4)+25$

$\left(x-(5)/(2)\right)^2+(y+5)^2=(-72+25+100)/(4)$

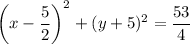
$\left(x-(5)/(2)\right)^2+(y+5)^2=(53)/(4)$

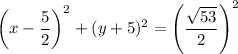$\left(x-(5)/(2)\right)^2+(y+5)^2=\left((√(53))/(2)\right)^2$ ...(ii)

On comparing (i) and (ii), we get

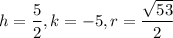
h=(5)/(2),k=-5,r=(√(53))/(2)

Therefore, the center is
$\left((5)/(2),-5\right)$ and the radius is
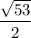units.