Question

If we list all the natural numbers below 10 that are multiples of 3 or 5, we get 3, 5, 6 and 9. the sum of these multiples is 23. find the sum of all the multiples of 3 or 5 below 1000.

Answer 1

this is a disguised sum of geometric sequence (2 of them)
find the largest number that is a multiplule of 3 and less than 1000 (999)
also largest number taht is multiplule of 5 and less than 1000 (995)
find the aritmetic sequence to generate each

an=a1+d(n-1)
a1=first term
d=common differnce

for the 3 one
first term is 3
a1=3
then d=3 as well
find
an=999=3+3(n-1)
n=333, the 333rd term

the 5's
first term is 5
common differnce is 5
an=5+5(n-1)
solve for n such taht
an=995=5+5(n-1)
n=199
199th term


sum of areitmetic sequence with an=nth term, n=which one, and a1=first

`S_n= (n(a_1+a_n))/(2)`

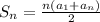
so the 3's
a1=3
an=999
n=333

`S_(333)= (333(3+999))/(2)`

`S_(333)= (333(1002))/(2)`

`S_(333)= 166833`

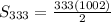
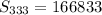
now the 5's
a1=5
an=995
n=199

`S_(199)= (199(5+995))/(2)`

`S_(199)= 99500`

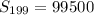
so add the 5's and 3's

166833+99500=266333

that is the sum of all the multipules of 3 and 5 below 1000