Question

What is the sum of the geometric sequence 1, 3, 9, ... if there are 13 terms

a 123,201
b 164,268
c 797,161
d 818,573

Answer 1

sum of geometric sequence where firts term is a1 andthe common ratio is r and the term you are summing to is n is


`S_n= (a_1(1-r^n))/(1-r)`
first term is 1
1 times 3=3
3 times 3=9
common ratio=3=r
13 terms, n=13


`S_(13)= (1(1-3^(13)))/(1-3)`

`S_(13)= (1-1594323)/(-2)`

`S_(13)= (-1594322)/(-2)`
S13=797161

C is answer

Answer 2

Answer: c. 797161

Explanation:

Here, the given geometric sequence,

1, 3, 9, ...

And, total number of the terms , n = 13.

first term, a = 1, and the common ratio,
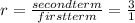`r = (second term )/(first term) = (3)/(1)` = 3

Since, the sum of the geometric series,

`S_n = (a(r^n-1))/(r-1)`

⇒
`S_(13) = (1 (3^(13)-1))/(3-1)`

⇒
`S_(13) = (1594323-1)/(3-1)`

⇒
`S_(13) = (1594322)/(2)`

⇒
`S_(13) = 797161`

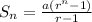
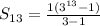
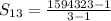
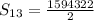
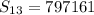
Thus, the sum of the given geometric series is 797161.

Therefore, Option C is correct.