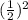Answer:
The required term is
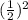
Step-by-step explanation:
Given : Equation
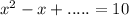
To find : What constant term should be added to both sides to complete the square on the left side?
Solution :
The quadratic equation is in the form

To complete the square we have to add the term

If we compare the equation, b=-1
So, The term has to add is
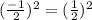
Substitute the term in the equation as adding it on both side,
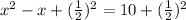
Now, we solve to make a complete square,
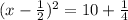

Therefore, The required term is