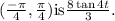Answer with explanation:
The parametric equation of same Ellipse is
x=3 cos t and y=8 sin t
x=3 cos 4 t and y = 8 sin 4 t
The equation of the ellipse is
![\rightarrow[(x)/(3)]^2+[(y)/(8)]^2=\cos^2 t +\sin^2 t \text{or} \cos^2 4t +\sin^2 4t\\\\(x^2)/(9)+(y^2)/(64)=1](https://img.qammunity.org/2018/formulas/mathematics/high-school/kjqbzde691bk4u6qzwpti5vuul7v0uf7j1.png)
The difference here is
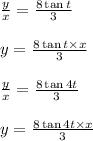
Both the parametric equation represent lines in two variable, both passing through origin.
→Slope of , parametric function, having period , (- π, π), that is x=3 cos t and y=8 sin t

→And slope of parametric function,x=3 cos 4t and y = 8 sin 4t having period