Question

The degree of the function f(x) = -(x + 1)2(2x − 3)(x + 2)2 is , and its y-intercept is

Answer 1

If you multiply everything the highest degree of x, which give the degree of the polynomial should be 5.
To find the y intercept you make x = 0
y int = - (1) ^2 (-3)(2)^2 = 12

Answer 2

Answer: The degree of the function is 5 and its y-intercept is (0, 12).

Step-by-step explanation: We are given to find the degree and the y-intercept of the following polynomial function:

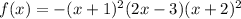`f(x)=-(x+1)^2(2x-3)(x+2)^2`~~~~~~~~~~~~~~~~~~~~~~~(i)[/tex]

To find the degree, we need to find the highest degree term in the polynomial.

The expanded form of the given polynomial (i) is

`P\\\\=-(x+1)^2(2x-3)(x+2)^2\\\\=-(x^2+2x+1)(2x-3)(x^2+4x+4)\\\\=-(x^2+2x+1)(2x^3+8x^2+8x-3x^2-12x-12)\\\\=-(x^2+2x+1)(2x^3+5x^2-4x-12)\\\\=-(2x^5+5x^4-4x^3-12x^2+4x^4+10x^3-8x^2-24x+2x^3+5x^2-4x-12)\\\\=-2x^5-9x^4-8x^3+15x^2+28x+12.`

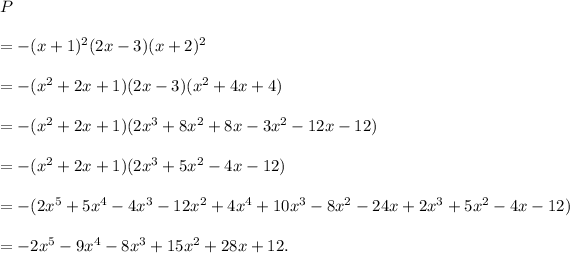
Since the highest power of x is 5, so the degree of the polynomial is 5.

Now, the y-intercept of a quadratic equation is a point where the x co-ordinate is 0.

So, the y-intercept of the function will be found by substituting the value of x as 0.

So, from equation (i), we have

`f(0)=-(0+1)^2(2*0-3)(0+2)^2=(-1)*(-3)*4=12.`

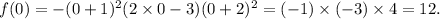
Thus, the degree of the function is 5 and its y-intercept is (0, 12).