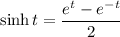Question

Find the Laplace Transform of y''+7y'+7y given that y(0)=0 and y'(0)=7

Answer 1

Assuming you start with the homogeneous ODE,


`y''+7y'+7y=0`

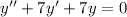
upon taking the Laplace transform of both sides, you end up with


`\mathcal L\left\{y''+7y'+7y\right\}=\mathcal L\{0\}`

`\mathcal L\{y''\}+7\mathcal L\{y'\}+7\mathcal L\{y\}=0`

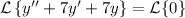
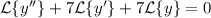
since the transform operator is linear, and the transform of 0 is 0.

I'll denote the Laplace transform of a function
`y(t)` into the
`s`-domain by
`\mathcal L_s\{y(t)\}:=Y(s)`.

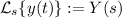
Given the derivative of
`y(t)`, its Laplace transform can be found easily from the definition of the transform itself:


`Y(s)=\displaystyle\int_0^\infty y(t)e^(-st)\,\mathrm dt`

`\implies\mathcal L_s\{y'(t)\}=\displaystyle\int_0^\infty y'(t)e^(-st)\,\mathrm dt`

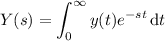
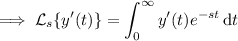
Integrate by parts, setting


`u=e^(-st)\implies\mathrm du=-se^(-st)\,\mathrm dt`

`\mathrm dv=y'(t)\,\mathrm dt\implies v=y(t)`

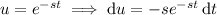
so that


`\mathcal L_s\{y'(t)\}=y(t)e^(-st)\bigg|_(t=0)^(t\to\infty)+s\displaystyle\int_0^\infty y(t)e^(-st)\,\mathrm dt`

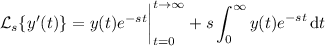
The second term is just the transform of the original function, while the first term reduces to
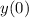
`y(0)` since
`e^(-st)\to0` as
`t\to\infty`, and
`e^(-st)\to1` as
`t\to0`. So we have a rule for transforming the first derivative, and by the same process we can generalize it to any order provided that we're given the value of all the preceeding derivatives at
`t=0`.

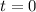
The general rule gives us


`\mathcal L_s\{y(t)\}=Y(s)`

`\mathcal L_s\{y'(t)\}=sY(s)-y(0)`

`\mathcal L_s\{y''(t)\}=s^2Y(s)-sy(0)-y'(0)`

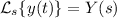
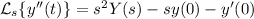
and so our ODE becomes


`\bigg(s^2Y(s)-sy(0)-y'(0)\bigg)+7\bigg(sY(s)-y(0)\bigg)+7Y(s)=0`

`(s^2+7s+7)Y(s)-7=0`

`Y(s)=\frac7{s^2+7s+7}`

`Y(s)=(14)/(√(21))\frac{\frac{√(21)}2}{\left(s+\frac72\right)^2-\left(\frac{√(21)}2\right)^2}`

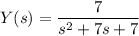
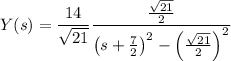
Depending on how you learned about finding inverse transforms, you should either be comfortable with cross-referencing a table and do some pattern-matching, or be able to set up and compute an appropriate contour integral. The former approach seems to be more common, so I'll stick to that.

Recall that


`\mathcal L_s\{\sinh(at)\}=\frac a{s^2-a^2}`

and that given a function
`y(t)` with transform
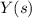
`Y(s)`, the shifted transform
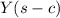
`Y(s-c)` corresponds to the function
`e^(ct)y(t)`.

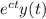
We have


`Y(s)=(14)/(√(21))\frac{\frac{√(21)}2}{\left(s+\frac72\right)^2-\left(\frac{√(21)}2\right)^2}`

`\implies Y\left(s-\frac72\right)=(14)/(√(21))\frac{\frac{√(21)}2}{s^2-\left(\frac{√(21)}2\right)^2}`

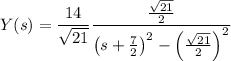
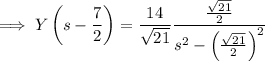
and so the inverse transform for our ODE is


`\mathcal L^(-1)_t\left\{Y\left(s-\frac72\right)\right\}=(14)/(√(21))\mathcal L^(-1)_t\left\{\frac{\frac{√(21)}2}{s^2-\left(\frac{√(21)}2\right)^2}\right\}`

`\implies e^(7/2t)y(t)=(14)/(√(21))\sinh\left(\frac{√(21)}2t\right)`

`\implies y(t)=(14)/(√(21))e^(-7/2t)\sinh\left(\frac{√(21)}2t\right)`

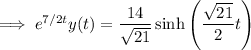
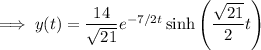
and in case you're not familiar with hyperbolic functions, you have


`\sinh t=\frac{e^t-e^(-t)}2`