Question

A frog sits at one end of a table which is 2m long. In its first jump the frog goes a distance of 1m along the table, with its second jump 1/2 m, with its third jump 1/4 m and so on. After how many jumps will the frog be within 1 cm of the far end of the table?

Answer 1

ah, this is an infinite sum question, or a sum of geometric sequence
when will the sum reach 1cm of the edge or about 1.99m
so

2m=200cm
within 1cm means at least 1.99m
so
we will use m and not cm for consitancy

sum of geometric sequence is

`S_n= (a_1(1-r^n))/(1-r)`
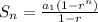
a1=first term=initial jjump=1
r=common ratio=1/2
n=?, we ar solving for that

so
we want it to equal 1.99 so


`1.99= (1(1- ((1)/(2))^n))/(1-(1)/(2))`

`1.99= ((1- ((1)/(2))^n))/((1)/(2))`

`1.99= 2(1- ((1)/(2))^n)`
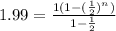
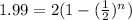
divide both sides by 2

`(1.99)/(2) = 1- ((1)/(2))^n`
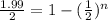
times -1

`(-1.99)/(2) = ((1)/(2))^n-1`
add 1 or 2/2 to both sides

`(0.01)/(2) = ((1)/(2))^n`
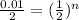
take the ln of both sides

`ln((0.01)/(2)) = ln(((1)/(2))^n)`

`ln((0.01)/(2)) = n ln((1)/(2))`
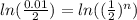
divide both sides by ln(1/2)

`(ln((0.01)/(2)))/(ln((1)/(2))) =n`
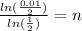
use your calculatro to find that n≈7.64386
so on 7th jump, it is not yet at 1cm to the edge but at 8th jump, it is past
so 8th jump