Answer:
$8,358.72
Explanation:
We know the formula for the compound interest given by,
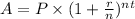 , where P = principle amount, r = rate of interest, n = number of times interest is compounded and t = time period.
, where P = principle amount, r = rate of interest, n = number of times interest is compounded and t = time period.
It is given that he principle amount at the start of the year is $2600 and for the first 5 months, the rate of interest is 4.3% i.e. 0.043.
Moreover, the credit card is compounded monthly.
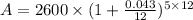
i.e.

i.e.

i.e.
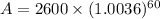
i.e.

i.e.
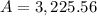
Therefore, the principle amount at the start of the 6th month is $3,225.56 and for the next ( 12-5 ) = 7 months, the rate of interest is 13.7% i.e. 0.137.
So, the amount compounded monthly for the next few months is,
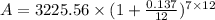
i.e.
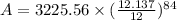
i.e.
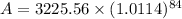
i.e.
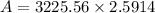
i.e.
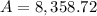
Hence, we get that Olive's balance at the end of the year is $8,358.72.