Question

A rectangular plece of paper with length 31 cm and width 14 cm has two semicircles cut out of it, as shown below. Find the area of the paper that remains. Use the value 3.14 for π, and do not round your answer. Be sure to include the correct unit in your answer.

Answer 1

Since the rectangular piece of paper has two halves of a circle cut out, then to find the remaining area you can subtract the area of ​​the rectangle minus the area of ​​the circle.

`A_{\text{remains}}=A_{\text{ rectangle}}-A_{\text{ circle}}`

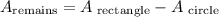
The formula to find the area of ​​a rectangle is:

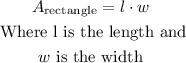
`\begin{gathered} A_{\text{rectangle}}=l\cdot w \\ \text{ Where l is the length and} \\ w\text{ is the width} \end{gathered}`

The formula to find the area of a circle is:

`\begin{gathered} A_{\text{circle}}=\pi r^2 \\ \text{ Where r is the radius of the circle} \end{gathered}`
`\begin{gathered} \pi\approx3.14 \\ r=7\text{ cm} \\ \text{ Because }r=(d)/(2)\text{ where d is the diameter of the circle} \end{gathered}`
`\begin{gathered} A_{\text{circle}}=\pi r^2 \\ A_{\text{circle}}=3.14\cdot(7cm)^2 \\ A_{\text{circle}}=3.14\cdot49cm^2 \\ A_{\text{circle}}=153.86cm^2 \end{gathered}`

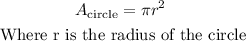
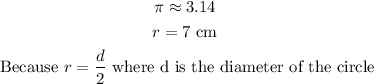
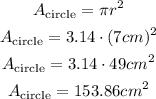
Finally, the area of the paper that remains is 280.14 cm².