Question

Divid 15 into two parts such that the sum of their reciprocal is 3/10

Answer 1

From the information obtained from the question, two equations can be created:

Let x and z be the two numbers (parts)


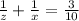
`(1)/(z) + (1)/(x) = (3)/(10)` . . . . (1)


`z + x = 15` . . . . (2)

By transposing (2), make 'z' the subject of the equation

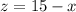
`z = 15 - x` . . . . (3)

By substituting (3) into equation (1) to find a value for x

`(1)/((15 - x)) + (1)/(x) = (3)/(10)`


`(15)/(( 15 - x ) ( x )) = (3)/(10)`


`3 ( - x^(2) + 15 x ) = 150`


`3 x^(2) - 45x + 150 = 0`

⇒
`( x - 5 ) ( x - 10 ) = 0`

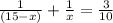
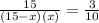
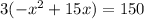
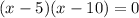
∴ either
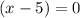
`( x - 5) = 0` OR
`( x - 10 ) = 0`

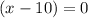
Thus x = 5 or x = 10

By substituting the values of x into (2) to find z

z + (5) = 15 OR z + (10) = 15

⇒ z = 10 OR z = 5

So, the two numbers or two parts into which fifteen is divided to yield the desired results are 5 and 10.