Answer:
The difference between the magnitudes of the earthquakes is 3.
Explanation:
We are given that,
The amplitude of large earthquake is 1000 times the amplitude of small earthquake.
That is,
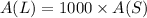
It is required to find the difference between magnitudes of the larger and smaller earthquakes.
We have the formula,

i.e.
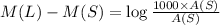
i.e.

i.e.

Thus, the difference between the magnitudes of the earthquakes is 3.