Answer: The required sum is 39991.
Step-by-step explanation: We are given to find the sum of the following 7-term geometric sequence:
1, -6, 36, . . ..
Here, the first term , a = 1
and
common ratio, 'r' is given by
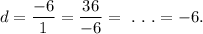
We know that
the sum of first 'n' terms of a geometric sequence is given by
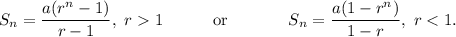
For the given geometric sequence, r = -6 < 1.
Therefore, the sum of first 7 terms will be
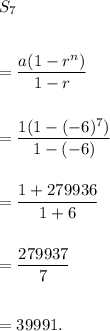
Thus, the required sum is 39991.