Question

What is the inter-quartile range of the given data set?
2
3
6

Answer 1

The answer is 3. To find the interquartile range, all you have to do is subtract your Q3-Q1. In this case, all you do is
20-17=3

Answer 2

Option 2 is correct. The inter-quartile range of the given data set is 3.

Explanation:

The left end of the box in a box plot represents the first quartile and right end of the box represents the third quartile.

From the given box plot is is clear that

`Q_1=17`

`Q_3=20`

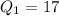
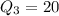
Inter-quartile range of the given data set is the difference between third quartile and first quartile.

`I.Q.R.=Q_3-Q_1`

`I.Q.R.=20-17=3`

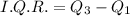
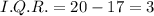
Therefore the inter-quartile range of the given data set is 3 and option 2 is correct.