Question

The height of one square pyramid is 24 m. A similar pyramid has a height of 8 m. The volume of the larger pyramid is 648 m3. Determine each of the following, showing all your work and reasoning:

(a) Scale factor of the smaller pyramid to the larger pyramid in simplest form

I think this first question is 1/3

(b)Ratio of the areas of the bases of the smaller pyramid to the larger pyramid


(c)Ratio of the volume of the smaller pyramid to the larger pyramid


(d)Volume of the smaller pyramid

Answer 1

`\bf \qquad \qquad \textit{ratio relations} \\\\ \begin{array}{ccccllll} &Sides&Area&Volume\\ &-----&-----&-----\\ \cfrac{\textit{similar shape}}{\textit{similar shape}}&\cfrac{s}{s}&\cfrac{s^2}{s^2}&\cfrac{s^3}{s^3} \end{array} \\\\ -----------------------------\\\\ \cfrac{\textit{similar shape}}{\textit{similar shape}}\qquad \cfrac{s}{s}=\cfrac{√(s^2)}{√(s^2)}=\cfrac{\sqrt[3]{s^3}}{\sqrt[3]{s^3}}\\\\ -----------------------------\\\\`


`\bf a) \\\\\\ \cfrac{small}{large}\qquad \cfrac{8}{24}\implies \cfrac{1}{3}\\\\ -----------------------------\\\\ b) \\\\\\ \cfrac{small}{large}\qquad \cfrac{8^2}{24^2}\implies \cfrac{64}{576}\implies \cfrac{1}{24}\\\\ -----------------------------\\\\ c) \\\\\\ \cfrac{small}{large}\qquad \cfrac{8^3}{24^3}\implies \cfrac{512}{13824}\implies \cfrac{1}{27}\\\\ -----------------------------\\\\ d) \\\\\\ \cfrac{small}{large}\qquad \cfrac{8^3}{24^3}=\cfrac{v}{648}\implies \cfrac{512}{13824}=\cfrac{v}{648}`

on d), solve for "v"

Answer 2

Answer: The answers are

(a)
`(1)/(3),`

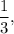
(b) 1 : 9,

(c) 1 : 27,

(d) 24 m³.

Step-by-step explanation: Given that the height of one square pyramid is 24 m and a similar pyramid has a height of 8 m. The volume of the larger pyramid is 648 m³.

Let, h and h' represents the heights of the smaller and the larger pyramid respectively.

Also, let V and V' be the volumes of the smaller and larger pyramid respectively.

Then, h = 8 m, h' = 24 m and V' = 648 m³.

(a) We know that the scale factor is defined by

`S=\frac{\textup{length of a side of the dilated figure}}{\textup{length of the corresponding side of the original figure }}.`

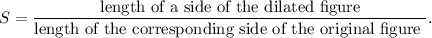
Therefore, the scale factor of the smaller pyramid to the larger pyramid will be

`S=\frac{\textup{h}}{\textup{h'}}=(8)/(24)=(1)/(3).`

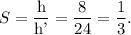
Thus, the required scale factor is
`(1)/(3).`

(b) We have

the ratio of the ares of the bases of the smaller pyramid to the larger pyramid is given by the ratio of the square of the lengths of two corresponding sides of the pyramids.

Therefore, the ratio of the ares of the bases of the smaller pyramid to the larger pyramid is

`(b)/(b')=(h^2)/(h'^2)=(8^2)/(24^2)=(1)/(3*3)=(1)/(9)\\\\\\b:b'==1:9.`

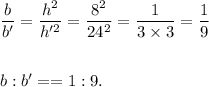
(c) We have

the ratio of the volume of the smaller pyramid to the larger pyramid is given by the ratio of the cubes of the lengths of two corresponding sides of the pyramids.

Therefore, the ratio of the volumes of the smaller pyramid to the larger pyramid is

`(V)/(V')=(h^3)/(h'^3)=(8^3)/(24^3)=(1)/(3*3*3)=(1)/(27)\\\\\\V:V'==1:27.`

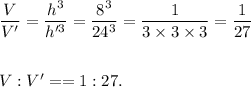
(d) V = ?

We have

`(V)/(V')=(1)/(27)\\\\\\\Rightarrow (V)/(648)=(1)/(27)\\\\\\\Rightarrow V=(648)/(27)\\\\\\\Rightarrow V=24~\textup{m}^3.`

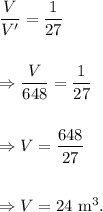
Thus, the required volume of the smaller pyramid is 24 m³.

All the questions are answered.