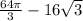Question

Express answer in exact form. Show all work for full credit.

A segment of a circle has a 120 arc and a chord of 8in. Find the area of the segment.

Answer 1

Our aim is to calculate the Radius so that to use the formula related to the area of a segment of a circle, that is: Aire of segment = Ф.R²/2

Let o be the center of the circle, AB the chord of 8 in subtending the arc f120°

Let OH be the altitude of triangle AOB. We know that a chord perpendicular to a radius bisects the chord in the middle. Hence AH = HB = 4 in

The triangle HOB is a semi equilateral triangle, so OH (facing 30°)=1/2 R. Now Pythagoras: OB² = OH² + 4²==> R² = (R/2)² + 16
R² = R²/4 +16. Solve for R ==> R =8/√3

OB² = OH² +

Answer 2

Explanation:

Given that a segment of a circle has a 120 arc and a chord of 8in.

Consider the triangle formed by two radii and the chord of 8 inches. This triangle is isosceles with two sides as equal radii. Hence each base angle is 30 degrees.

By sine formula for triangles

`(r)/(sin30) =(8)/(sin120) \\r = (8√(3) )/(3)`

Area of segment = area of sector - area of triangle

Area of sector =
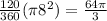`(120)/(360) (\pi 8^2) = (64\pi)/(3)` ... I

Area of triangle =
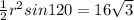`(1)/(2) r^2 sin 120 =16√(3)` ...II

Hence area of segment = I-II =
`(64\pi)/(3)-16√(3)`