Question

Show in each case that the series converges or diverges

Answer 1

I can't make out the summand in (d), and I addressed (c) in your other question.

(a)
`\displaystyle\sum_(n\ge1)(\cos n\pi)/(n\sqrt n)`

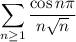
We have for positive integers
`n` that
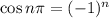
`\cos n\pi=(-1)^n`. We also are aware that the series


`\displaystyle\sum_(n\ge1)\frac1{n^(3/2)}`

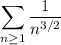
converges, since it is a
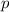
`p`-series with
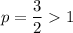
`p=\frac32>1`. Since the
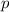
`p`-series converges in absolute value, the alternating series must also converge by comparison.

- - -

(b)
`\displaystyle\sum_(n\ge1)(-1)^n\frac{\ln n}n`

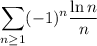
By the alternating series test, this series will converge if the absolute value of the summand is increasing for some large enough
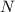
`N` and approaches zero.

We have


`\left|(-1)^n\frac{\ln n}n\right|=\frac{\ln n}n>0`

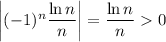
for all
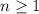
`n\ge1`, and we also have that


`\displaystyle\lim_(n\to\infty)\frac{\ln n}n=\lim_(m\to\infty)\frac m{e^m}=0`

(where we substituted
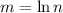
`m=\ln n`, so that
`e^m=n`).

Therefore (b) also converges.