Answer:
b) Quadratic Formula
Explanation:
The given expression is :
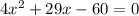
We will solve this by using Quadratic Equation Formula.
When the equation is in the form of
 we use the formula:
we use the formula:
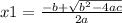 and
and
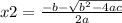
Here a = 4, b = 29 and c = -60
Putting these in formula we get:
 and
and
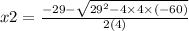
Solving these we get,
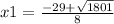 and
and
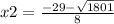
The final answer are :
x1=1.6797
x2=-8.9297
So, the quadratic formula is used here.
Factorization is not possible as the given equation is not a perfect square.
Taking the Square Root method will also not work here as this method helps when the expression contains only
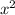 term.
term.