Question

According to a survey, 15% of city workers take the bus to work. Donatella randomly surveys 10 workers. What is the probability that exactly 6 workers take the bus to work? Round the answer to the nearest thousandth.

A.0.001
B.0.002
C.0.128
D.0.900

Answer 1

X: the number of workers taking the bus to work
p: probability of success =(15/100) = 0.15
q: probability of failure =1- p = 0.85
P(X=6) = 10C6(0.15)^6(0.85)^4
= 0.001

Ans: A

Answer 2

Answer: Option 'A' is correct

Explanation:

Since we have given that 15% of city workers take the bus to work ,

We will use "Binomial Distribution"

`P(X=x)=^nC_kp^k(1-p)^(n-k)`

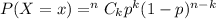
Here,

p denotes "Probability of success",

(1-p) denotes "Probability of failure",

n denotes the "number of workers"

k denotes "number of given workers"

So, Probability of success is given by

`p=(15)/(100)=0.15`

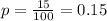
And, probability of failure is given by

`(1-p)=1-0.15=0.85`

Hence, our binomial distribution will look like

`^(10)C_6(0.15)^6(0.85)^4=0.001`

Hence, Option 'A' is correct.