Question

What is the maximum number of possible extreme values for the function, F(x)=x^3-7x-6

Answer 1

2 is the max number because it's one less than the degree

Answer 2

The maximum number of possible extreme values for the function,

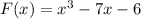`F(x)=x^3-7x-6` is:

2

Explanation:

By the Theorem of extreme values of a polynomial function we have:

The graph of a polynomial equation of degree n has atmost ( less than or equal to) "n-1" extreme values ( i.e. minima and/or maxima).

That means the total number of extreme values could be n-1, n-3, n-5 etc.

Hence, here we have a polynomial equation as:

`F(x)=x^3-7x-6`

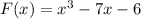
i.e. we have a polynomial function of degree 3 i.e. n=3

So, the maximum number of possible extreme values that may exits is: 2

( Since n-1=3-1=2)