Answer:
The required numbers are 5 and 20.
Explanation:
Given : One number is four times another number.
Let the first number is 'x'
The reciprocal of the first number is
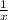
and another number is '4x'
The reciprocal of the another number is
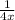
The sum of their reciprocals is
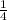
i.e.

Solving the equation,
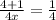

Cross multiply,
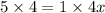
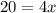
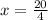

Another number is
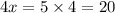
Therefore, the required numbers are 5 and 20.