Question

Find the inverse of the function. Is the inverse a function?

y = 5x^2 + 2

Answer 1

to find the inves
solve for x and replace x with finverse and y with x

y=5x^2+2
minus 2
y-2=5x^2
divide by 5
(y-2)/5=x^2
sqrt both sides

`x= \sqrt{(y-2)/(5) }`

`x= ( √( y-2))/( √(5) )`

`x= ( √(5( y-2)))/(5 )`

`x= ( √(5y-10))/(5 )`
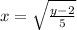
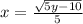
inverse

`f(x)^(-1)= ( √(5x-10))/(5 )`
for it to be a function, every x must corespond to exactly 1 y
seems to corespond to 1 each
it is a function

Answer 2

f^-1 (x)= sqrt(5x)/ sqrt(5x),  -sqrt(5x)/5 is the inverse of the function y=5x^2