Question

The sum of the two digits of a number is 16. The number formed by reversing the digits is 18 more than the original number. Determine the original number. Let t = the tens digit, u = the units digit, and u + t = 16. Which of the following equations would complete the system?

9t - 9u = 18
9u - 9t = 18
tu = ut + 18

Answer 1

9t-9u=18 is ur answer

Answer 2

`9u-9t=18`

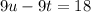
Explanation:

The equation that completes the system is:

`9u-9t=18`

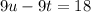
First, we have to remember that tens value 10 units per digit, and units value one uni per digit. So, the number of the problem would be expressed like:

`10t+u`

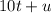
Now, the problem states that if the number is reversed its formed another number which is 18 units more than the original, that would be expressed like:

`10u+t=10t+u+18`

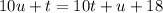
Solving this relation, we have:

`10u-u=10t-t+18\\9u=9t+18\\9u-9t=18`

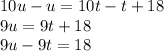
Therefore, the expression that complete the system is the second equation.