Question

Suppose a laboratory has a 31 g sample of polonium-210. The half-life of polonium-210 is about 138 days. How many half-lives of polonium-210 occur in 966 days? How much polonium is in the sample 966 days later?

Answer 1

A=P(1/2)^(t/h)
P=initial amount
t=time
h=half life
A=final amount
so

A=0.242188 grams

Answer 2

0.24 grams of polonium is in the sample 966 days later.

Explanation:

Given : Suppose a laboratory has a 31 g sample of polonium-210. The half-life of polonium-210 is about 138 days.

To find : How many half-lives of polonium-210 occur in 966 days? How much polonium is in the sample 966 days later?

Solution :

The half-life of polonium-210 is about 138 days.

We have to find the number of half-lives of polonium-210 occur in 966 days.

The number of half-lives is
`n=(966)/(138)=7`

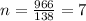
The amount of polonium-210 remaining after t days is given by the equation,

`N(t)=N_0* ((1)/(2))^{\frac{t}{t_{(1)/(2)}}`

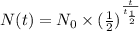
where,

N(t) is the amount of substance remaining after t days,

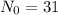`N_0=31` is the initial amount of substance,

t=966 is the time in days,

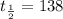`t_{(1)/(2)}=138` is the half-life of the substance.

Substitute the values in the formula,

`N(t)=31 * ((1)/(2))^{(966)/(138)`

`N(t)=31 * ((1)/(2))^(7)`

`N(t)=31 * 0.0078125`

`N(t)=0.24`

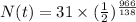
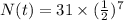
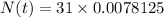
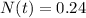
Therefore, 0.24 grams of polonium is in the sample 966 days later.