SOLUTION
In a right angle triangle, the hypotenuse is always the side opposite the right angle
Hence, from the image given,
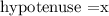
Apply pythagoras rule i.e the square of the hypotenuse side is equal to the sum of squares of the other two sides“
we have
![x^2=3^2+(2\sqrt[]{2})^2](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/4s7daom1tn6tdql3f09o.png)
Simplify the expression above

Take the square root of both sides
![\begin{gathered} \sqrt[]{x^2}=\sqrt[]{17} \\ \text{Then} \\ x=\sqrt[]{17}in \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/cz42pa7fl7xyxrgst5t2.png)
Hence
The missig side in the triangle is √17in
Answer: √17in