(a)
The profit function, P(x), is
Profit = Revenue - Cost
So,
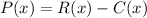
We can find the simplified profit function, shown below:
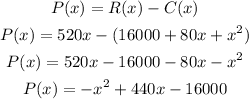
(b)
To find the profit when 30 units are sold, we substitute x = 30 into the profit function.
So,
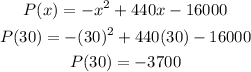
So, there is a loss of $3700.
Or, profit of $ -3700
(c)
To find the profit when 45 units are sold, we substitute x = 45 into the profit function.
So,
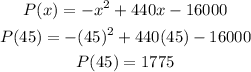
The profit is $ 1775
(d)
Break Even is the point where Revenue equal Cost.
So,

Let's find the number of units to break-even,
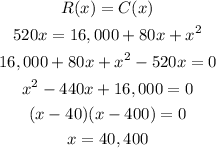
For x = 40 units, it will break even.