Question

Bart found 20 quadrilaterals in his classroom. He made a Venn diagram using the properties of the quadrilaterals, comparing those with four equal side lengths (E) and those with four right angles (R).

Given that a randomly chosen quadrilateral has four right angles, what is the probability that the quadrilateral also has four equal side lengths? Express your answer in percent form, rounded to the nearest whole percent.

___%

Answer 1

The correct answer is:

A. 25%

Given that a randomly chosen quadrilateral has four right angles, the probability that the quadrilateral also has four equal side lengths is 25%.

`|Huntrw6|`

Answer 2

Number of Quadrilateral made by Bart in the classroom = 20

R =Number of quadrilateral having four right angles = {Square , Rectangle}=2

E=Number of quadrilateral having four equal side lengths = { Rhombus, Square}=2

Total favorable outcome =4 if quadrilateral with special properties are selected

Or

Total favorable outcome = 20 , if all quadrilateral is selected.

Out of Randomly selected quadrilateral which has four right angles, the quadrilateral which has four equal side lengths = R ∩ E ={Square}=1

Required probability=
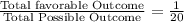`\frac{\text{Total favorable Outcome}}{\text{Total Possible Outcome}}=(1)/(20)` or
`(1)/(4)`.

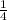Which is 5% if Total number of Quadrilateral = 20

And , 25% if total number of Quadrilateral selected = 4