Question

Where is the removable discontinuity of f(x)=x+5/x^2+3x-10 located

a. x=-5
b. x=-2
c. x=2
d. x=5

Answer 1

a.
`x=-5`

Explanation:

The discontinuity of an equation is when the denominator is equal to zero.

The denominator equation is a quadratic equation that is to say it has two possible points where x can be equal to zero (roots)

to find the roots of we use the quadratic formula

`f(x)=(x+5)/(x^2+3x-10)`

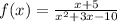
denominator:
`x^2+3x-10`

`a=1\\b=3\\c=-10\\ x = \frac {-b \pm \sqrt {b^2 - 4ac}}{2a}\\ x = \frac {-(3) \pm \sqrt {(3)^2 - 4(1)(-10)}}{2(1)}\\ x = \frac {-3 \pm \sqrt {9 +40}}{2}\\ x = \frac {-3 \pm \sqrt {49}}{2}\\ x = \frac {-3 \pm7}{2} \\ x_1= \frac {-3 +7}{2}\\x_1= (4)/(2)\\ x_1= 2\\x_2=\frac {-3 -7}{2}\\x_2= -5`

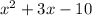
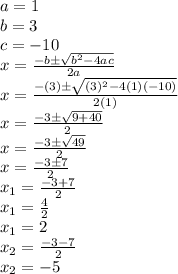
we clear the value of x from the numerator

`x=-5`

Is common for both the numerator and the denominator we can cancel it and the discontinuity is removable

Answer 2

We are tasked to solve for the removable discontinuity of the expression below:
f(x) = (x+5) / (x²+3x-10)

Factoring the denominator, we have:
f(x) = y = (x+5) / (x+5)(x-2)

Canceled out (x+5) which is common in numerator and denominator, we have:
y = 1 / (x-2)

Removable discontinuity is (x+5) or x= -5. The answer is the letter "A".