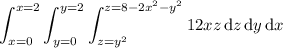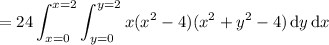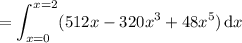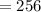The intersection of the two surfaces occurs along the cylinder
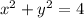
, so we have the

- and
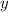
-coordinates of the points in the bounded region contained within
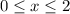
and
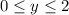
, while
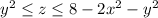
.
The triple integral is then given by
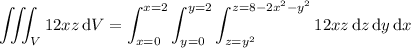
where
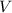
denotes the bounded region in the first quadrant.
Integrating in Cartesian coordinates is easy enough to do in this order.