Answer:
Option D - It is horizontally compressed by a factor of 2 and reflected over the y-axis.
Explanation:
Given : The graph of
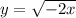 related to its parent function
related to its parent function
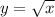 .
.
To find : How is the graph translated?
Solution :
Let,
The parent function
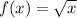
Translated function

- In the parent function, the graph is reflected over y-axis as
The reflection of the point (x,y) across the y-axis is the point (-x,y).
f(x,y)→f(-x,y)
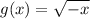
- In the parent function, the graph is horizontally compressed as
The compression horizontally the function became
y=f(x)→ y=f(bx) , b is the compression factor and b>1
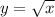 →
→
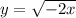 , function is compressed by 2 unit.
, function is compressed by 2 unit.
Therefore, Option D is correct.
It is horizontally compressed by a factor of 2 and reflected over the y-axis.
We plot the graph of both the equations in which translation is shown.
Refer the attached graph below.