Question

A company's board of directors wants to form a committee of 3 of its members. There are 6 members to choose from. How many different committees of 3 members could possibly be formed?

Answer 1

order doesn't mater so use combinations:
6C3 = 6!/ (3! (6-3)! ) = 6! /(3!*3!) = 6*5*4*3! / (3! 3!) = 6*5*4/3*2*1) = 20

Answer 2

Total 20 different committees of 3 members could possibly be formed.

Explanation:

Given information:

Total number of members = 6

Total number of members who are selected = 3

Total number of ways to select r items from n items is

`^nC_r=(n!)/(r!(n-r)!)`

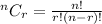
Total number of ways to select 3 members from 6 members is

`^6C_3=(6!)/(3!(6-3)!)`

`^6C_3=(6* 5* 4* 3!)/(3* 2* 1* (3)!)`

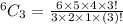
Cancel out the common factors.

`^6C_3=(6* 5* 4)/(3* 2* 1)`

`^6C_3=20`

Therefore total 20 different committees of 3 members could possibly be formed.