Question

Write the equation of a circle with a center at (1, 4) where a point on the circle is (4, 8).

a. (x - 4)2 + (y - 1)2 = 25
b.(x - 1)2 + (y - 4)2 = 25
c. (x - 1)2 + (y - 4)2 = 5
d.(x + 1)2 + (y + 4)2 = 25

Answer 1

First find the radius which is the Distance from the Center to the Circumference of the circle, using the distance formula:
D^2 = (1-4)^2 + (4-8)^2 = 9+ 16 =25
D = 5 = R

R^2 = (x-h)^2 + (y-k)^2
25 = (x-1)^2 +(y-4)^2 B

Answer 2

B) (x - 1)² + (y - 4)² = 25.

Explanation:

Given : A circle with a center at (1, 4) where a point on the circle is (4, 8).

To find : Write the equation of a circle.

Solution : We have given that center (1 ,4)

A point on a circle (4 ,8).

Distance between center and point on circle is called diameter .

Distance formula :
`\sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)}`.

Diameter =
`\sqrt{(4-1)^(2)+(8-4)^(2)}`.

Diameter =
`\sqrt{(3)^(2)+4)^(2)}`.

Diameter =
`√(9 +16)`.

Diameter =
`√(25)`.

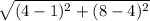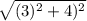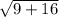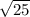Diameter = 5.

Radius = 2.5

Equation of center = (x - h)² + (y - k)² = r².

Where , (h , k) in coordinates of center and r is radius.

Equation of circle : (x - 1)² + (y - 4)² = 5².

(x - 1)² + (y - 4)² = 25.

Therefore, B) (x - 1)² + (y - 4)² = 25.