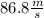Question

A projectile is fired from the top of a 120 m tall building with an initial velocity of Vi = 72.0 m/s and an initial angle theta i =25.0° above the horizontal.Answer the following questions. [Use g= 9.80 m/s^2]Question 13What is the speed of the projectile the moment it touches the ground?Round your answer to 3 significant figures.

Answer 1

The vertical component of the speed changes uniformly with time as follows:

`v_y=v_(0y)-gt`

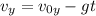
The horizontal component of the speed remains constant:

`v_x=v_(0x)`

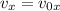
To find the initial values for the components of the speed, remember the following:

`\begin{gathered} v_(0y)=v_0\sin (\theta) \\ v_(0x)=v_0\cos (\theta) \end{gathered}`

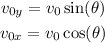
Substitute the values for v₀ and θ:

`\begin{gathered} v_(0y)=72.0(m)/(s)*\sin (25º)=30.4(m)/(s) \\ v_(0x)=72.0(m)/(s)*\cos (25º)=65.3(m)/(s) \end{gathered}`

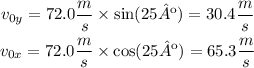
Since the projectile touches the ground at time t=8.95s, use that value to find the final vertical speed:

`\begin{gathered} v_y=v_(0y)-gt \\ =(30.4(m)/(s))-(9.80(m)/(s^2))(8.95s) \\ =-57.3(m)/(s) \end{gathered}`

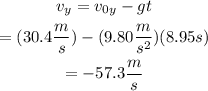
The final speed of the projectile when it touches the ground is given by:

`\begin{gathered} v=\sqrt[]{v^2_x+v^2_y} \\ =\sqrt[]{(65.3(m)/(s))^2+(-57.3(m)/(s))^2} \\ =86.8(m)/(s) \end{gathered}`

Therefore, the speed of the projectile the moment it touches the ground, is:

`86.8(m)/(s)`