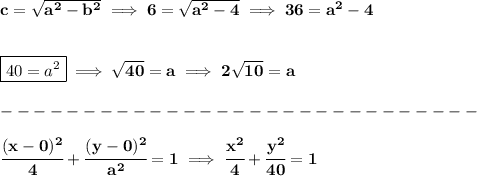Question

What is the equation of the ellipse with foci (0, 6), (0, -6) and co-vertices (2, 0), (-2, 0)?

Answer 1

so hmm if you check the picture below

those are the given foci and co-vertices

so, since the co-vertices are at 2,0 and -2,0 that makes the center, at the origin and the "b" component 2, so the minor axis is just 2+2 or 4

now, what's the major axis? or what is the "a" component?

based on the provided points, is a vertical ellipse, that means the major axis runs over the y-axis and thus the "a" or larger denominator, lies under the fraction with the "y"

now


`\bf \textit{ellipse, vertical major axis}\\\\ \cfrac{(x-{{ h}})^2}{{{ b}}^2}+\cfrac{(y-{{ k}})^2}{{{ a}}^2}=1 \qquad \begin{cases} center\ ({{ h}},{{ k}})\\ vertices\ ({{ h}}, {{ k}}\pm a)\\ c=\textit{distance from}\\ \qquad \textit{center to foci}\\ \qquad \sqrt{{{ a }}^2-{{ b }}^2}\\ ----------\\ h=0\\ k=0\\ b=2\\ c=6 \end{cases}`


`\bf c=√(a^2-b^2)\implies 6=√(a^2-4)\implies 36=a^2-4 \\\\\\ \boxed{40=a^2}\implies √(40)=a\implies 2√(10)=a\\\\ -----------------------------\\\\ \cfrac{(x-0)^2}{4}+\cfrac{(y-0)^2}{a^2}=1\implies \cfrac{x^2}{4}+\cfrac{y^2}{40}=1`