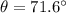Question

Find the angle between the given vectors to the nearest tenth of a degree.

u = <8, 4>, v = <9, -9>

Answer 1

`\bf \textit{angle between two vectors }\\ \quad \\ cos(\theta)=\cfrac{u \cdot v} \implies \cfrac{\text{dot product}}{\text{product of magnitudes}}\\ \quad \\\\ \theta = cos^(-1)\left(\cfrac{u \cdot v}v\right)\\\\ -----------------------------\\\\ \theta=cos^(-1)\left[ \cfrac{\ \textless \ 8,4\ \textgreater \ \quad \cdot \quad \ \textless \ 9,-9\ \textgreater \ }{(√(8^2+4^2))(√(9^2+(-9)^2))} \right]`



`\bf \theta=cos^(-1)\left[ \cfrac{(8\cdot 9)+(4\cdot -9)}{(√(64+16))(√(81+81))} \right]\implies \theta=cos^(-1)\left[ \cfrac{36}{(√(80))(√(162))} \right] \\\\\\ \theta=cos^(-1)\left[ \cfrac{36}{(√(80))(√(162))} \right]\implies \theta=cos^(-1)\left[ \cfrac{36}{√(12960)}\right] \\\\\\ \theta=cos^(-1)\left[ \cfrac{36}{36√(10)}\right]\implies \theta\approx 71.565^o`

Answer 2

`\theta=71.6^(\circ)`

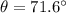
Explanation:

We are given that two vectors

u=<8,4> and v=<9,-9>

The given vectors can be write as

`\vec{u}=8\hat{i}+4\hat{j}`

`\vec{v}=9\hat{i}-9\hat{j}`

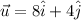
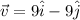
We have to find the angle between two given vectors

The formula to find out the angle between two vectors is given below

`cos\theta=\frac{\vec{u}\cdot\vec{v}}{\mid\vec{u}\mid\cdot \mid\vec{v}\mid}`

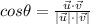
By applying this formula we have to find the angle between two vectors

`\mid{\vec{u}\mid=√(8^2+4^2)=√(64+16)=√(80)=4\sqrt5`

`\mid\vec{v}\mid=√(9^2+(-9)^2)=√(81+81)=9\sqrt2`

`\vec{u}\cdot\vec{v}=(8\hat{i}+4\hat{j})\cdot(9\hat{i}-9\hat{j})=72-36=36`

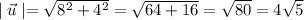
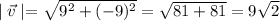
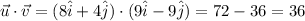
Using
`\hat{i}\cdot\hat{i}=1,\hat{j}\cdot\hat{j}=1,\hat{k}\cdot\hat{k}=1`

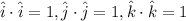
Substituting the values then we get

`cos\theta=(36)/(4\sqrt5\cdot9\sqrt2)`

`cos\theta=(1)/(\sqrt10)=(1)/(3.16)`

`cos\theta=0.3164`

`\theta=cos^(-1)(0.3164)=71.55^(\circ)`

`\theta=71.6^(\circ)`

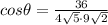
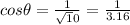
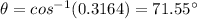
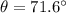
Answer:
`\theta=71.6^(\circ)`