Question

What is the sum of the roots of the polynomial shown below f(x)=x^3-8x^2-23x+30

Answer 1

f(1)=0 so x=1 is a zero => x-1 is a factor 1 | 1 -8 -23 30 | 1 -7 -30 --------------------- 1 -7 -30 | 0 x^2-7x-30 is another factor x^2-7x-30=(x-12)(x+5) x=12, x=-5 our roots too s0 1+12+(-5)=13-5=8

Answer 2

Answer: The sum of roots of the polynomial is 8.

Step-by-step explanation:

The given polynomial is,

`f(x)=x^3-8x^2-23x+30`

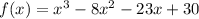
Use hit and trial method to find the one root. Since
`\pm1` is the possible rational root for each polynomial.

`f(1)=(1)^3-8(1)^2-23(1)+30=0`

Sicen at x=1 the value of f(x) is 0 therefore 1 is a root of the polynomial and (x-1) is a factor of the polynomial.

Use synthetic division or long division method to find the other factor of the polynomial.

`f(x)=x^3-8x^2-23x+30=(x-1)(x^2-7x-30)`

`f(x)=(x-1)(x^2-10x+3x-30)`

`f(x)=(x-1)(x(x-10)+3(x-10))`

`f(x)=(x-1)(x-10)(x+3)`

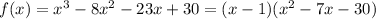
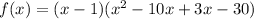
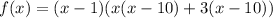
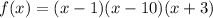
Equation each factor of f(x) equal to 0.

`x=-3,1,10`

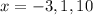
So, the roots are -3, 1, 10. Sum of roots is,

`-3+1+10=8`

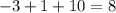
Therefore, the sum of roots of the polynomial is 8.