Question

what height is the rocket launched from?when does the rocket reach its maximum height?what is the maximum height reached by the rocket?how many seconds after it's launched will the rocket hit the lake?

Answer 1

We have that the movement of the rocket can be modeled with the following function:

`h(t)=-16t^2+64t+80`

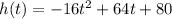
a)To find the height the rocket is launched from, we have to make t = 0, since that is the initial time, and evaluate h(0):

`\begin{gathered} t=0 \\ \Rightarrow h(0)=-16(0)^2+64(0)+80=80 \\ h(0)=80 \end{gathered}`

therefore, the rocket is launched from a height of 80 units.

b)To find the maximum height, notice that the function h(t) is a quadratic function, then we have to find the vertex of the parabolla that represents using the following expression:

`\begin{gathered} given\colon f(x)=ax^2+bx+c \\ vertex\colon(-(b)/(2a),f(-(b)/(2a))) \end{gathered}`

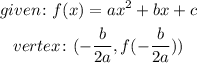
in this case, we have the following constants a,b and c:

`\begin{gathered} a=-16 \\ b=64 \\ c=80 \end{gathered}`

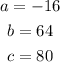
then, we can find the vertex using the expression above:

`\begin{gathered} -(b)/(2a)=-(64)/(2(-16))=-(64)/(-32)=2 \\ \Rightarrow f(-(b)/(2a))=f(2)=-16(2)^2+64(2)+80=-64+128+80=144 \\ vertex\colon(2,144) \end{gathered}`

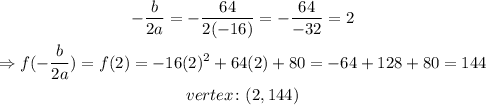
thus, the maximum height reached is 144 units after 2 seconds

c)Finally, to find out how many seconds it takes the rocket to hit the lake, we have to solve h(t) = 0:

`\begin{gathered} h(t)=0 \\ \Rightarrow-16t^2+64t+80=0 \end{gathered}`

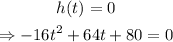
notice that all coefficients are divisible by -16, then, factoring we get:

`\begin{gathered} -16t^2+64t+80=0 \\ \Rightarrow-16(t^2-4t-5)=0 \\ \Rightarrow-16(t+1)(t-5)=0 \end{gathered}`

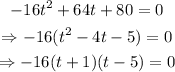
we can see that this equation has solutions t = -1 and t = 5. Since t = -1 cannot be posible, we have that after t = 5 seconds the rocket will hit the lake