Question

The depreciating value of a semi-truck can be modeled by y = Ao(0.85)x, where y is the remaining value of the semi, x is the time in years, and it depreciates at 15% per year. An exponential function comes down from the positive infinity and passes through the points zero comma seventy-five thousand. The graph is approaching the x-axis. What is the value of the truck initially, Ao, and how would the graph change if the initial value was only $65,000?

Answer 1

Explanation:

Given that the depreciating value of a semi-truck can be modeled by

`y = Ao(0.85)^x`

Since it crosses (0,75000) we find that when x =0 y = 75000

Substitute to get

`A_0 = 75000`

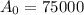
So equation would be

`y = 75000(0.85)^x`

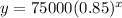
If initial value is changed to 65000, the y intercept would be shifted down to

65000. The whole curve would be a bit vertical down than the previous curve.

Answer 2

We are given the equation
y = Ao (0.85)^x

Initially, at x = 0, the value of y is
y = Ao (0.85)^0
y = Ao

If the initial value was $65,000 at the same rate of depreciation, the equation would be
y = 65000 (0.85)^x