Question

Two number cubes are rolled for two separate events:

All of the combinations of numbers on both cubes that give a sum less than 10.
All combinations of numbers on both cubes that give a sum that is a multiple of 3.

a. In terms of a reduced fraction, find the conditional probability of B given that A occurs first. Fill in the blanks P( __ l __ ) = __ / __

b. Complete the conditional-probability formula for event B given that event A occurs first by writing A and B in the blanks: P( __ l __ ) = P( __ ∩ __ ) / P( __ )

c. List the members of the sample space for event A ∩ B.

d. List the members of the sample space for event A.

Answer 1

To find the conditional probability of event B given that event A occurs first, we need to calculate the probability of A and B occurring together and divide it by the probability of event A occurring. The conditional probability formula is P(B l A) = P(A ∩ B) / P(A). I calculated the probability using the given information and obtained a fraction of 5/12.

Step-by-step explanation:

To find the conditional probability of event B given that event A occurs first, we need to calculate the probability of A and B occurring together and divide it by the probability of event A occurring. Let's fill in the blanks:

P(B l A) = P(A ∩ B) / P(A)

Event A is defined as rolling either a three or four first, followed by an even number. We can calculate the probability of A by dividing the favorable outcomes (2 outcomes) by the total number of possible outcomes (6 outcomes). So, P(A) = 2/6 = 1/3.

To calculate P(A ∩ B), we need to find the number of outcomes that satisfy both event A and event B. Event B is defined as the sum of the two rolls being at most seven. We can list all the outcomes that satisfy both conditions: {33, 34, 35, 42, 43}. There are 5 outcomes, so P(A ∩ B) = 5/36.

Now we can substitute the values into the formula: P(B l A) = (5/36) / (1/3) = 5/12.

Answer 2

Step-by-step explanation:

When two cubes are rolled then the favourable outcomes are: 36 (given below)

(1,1) ; (1,2) ; (1,3) ;(1,4) ; (1,5) ;(1,6)

(2,1) ; (2,2) ; (2,3) ;(2,4) ; (2,5) ;(2,6)

(3,1) ; (3,2) ; (3,3) ;(3,4) ; (3,5) ;(3,6)

(4,1) ; (4,2) ; (4,3) ;(4,4) ; (4,5) ;(4,6)

(5,1) ; (5,2) ; (5,3) ;(5,4) ; (5,5) ;(5,6)

(6,1) ; (6,2) ; (6,3) ;(6,4) ; (6,5) ;(6,6)

Favourable events of numbers on both cubes that give a sum less than 10 are (1,1) ; (1,2) ; (1,3) ;(1,4) ; (1,5) ;(1,6) ;(2,1) ; (2,2) ; (2,3) ;(2,4) ; (2,5) ;(2,6) ;(3,1) ; (3,2) ; (3,3) ;(3,4) ; (3,5) ;(3,6); (4,1) ; (4,2) ; (4,3) ;(4,4) ; (4,5);(5,1) ; (5,2) ; (5,3) ;(5,4) ;(6,1) ; (6,2) ; (6,3)

so total no. of favourable events of numbers on both cubes that give a sum less than 10 = 30

Probability of getting sum less than 10 =
`(30)/(36)`

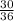
Favourable events of numbers on both cubes that give a sum that is a multiple of 3 are (1,3);(1,6);(2,3);(2,6);(3,1) ; (3,2) ; (3,3) ;(3,4) ; (3,5) ;(3,6);(4,3);(4,6);(5,3);(5,6);(6,1) ; (6,2) ; (6,3) ;(6,4) ; (6,5) ;(6,6)

so total no. of favourable events of numbers on both cubes that give a sum that is a multiple of 3 = 20

Probability of getting a multiple of 3=
`(20)/(36)`

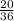
(A) P(B|A)= \frac{P(B∩A)}{P(A)} =
`(15/36)/(30/36)` =
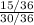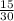`(15)/(30)`=0.5

(B)P(A|B)=
`(P(A∩B))/(P(B))`=
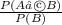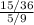`(15/36)/(5/9)`=0.75

(C) {A∩B} = {3, 6, 9, 12, 15, 18}

(D) {A} = {1, 2, 3, 4, 5 ,6, 7, 8, 9}l