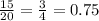Question

Eric surveys students at his school and finds that 80% have a pet. He wants to estimate the probability that, if he randomly selected 4 students, more than 2 would have a pet.

To estimate this probability, he lets the numbers 1, 2, 3, and 4 represent a student who has a pet and 5 represent a student who does not have a pet. He then has a computer randomly select 4 numbers and repeats this 20 times.

The results of these trials are shown in the table.

5533 2245 1555 3341
4252 5335 5321 4155
2131 3414 1532 4251
2523 3311 2352 2332
5451 3344 1121 5243
Based on this simulation, what is the estimated probability that more than 2 of 4 randomly selected students would have a pet?

Enter your answer, as a decimal, in the box.

Answer 1

0.75

Step by Step Explanation:

I took the quiz :)

Answer 2

1. The total number of experiments is 20

2. Call the 4 digit numbers a "string of numbers".

If a string has no 5', then all 4 students have pets
If a string has one 5, then 3 students have pets
If a string has two 5's, then 2 students have pets,
If a string has three 5's, then 1 student has pets

So only if a string has zero or one 5, then more than 2 of 4 students have pets.

We can count 15 stings with 0 or 1 five.


P(more than 2 of 4 students have a pet)=
`(n(more than 2 of 4 students have a pet))/(n(Experiments))`=
`(15)/(20)= (3)/(4)=0.75`