Question

Need some help I do not necessary want the answer but the process to get the answer, thank you.

Use the following graph of the function f(x) = 2x3 + x2 − 3x + 1 to answer this question:
What is the average rate of change from x = −2 to x = 0?

Answer 1

Given function :
`f(x) = 2x^3 + x^2-3x + 1`.

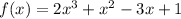We need to find the average rate of change from x = −2 to x = 0.

Let us find the values of y-coordinates for x=-2 and x=0 for the given function on the graph.

`f(-2) = 2(-2)^3 +(-2)^2-3(-2) + 1=-5`

`f(0)=\:2\left(0\right)^3\:+\left(0\right)^2-3\left(0\right)\:+\:1 =1`

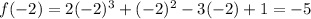
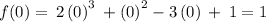
Formula for average rate of change is :

`f_(avg)=(f(b)-f(a))/(b-a)`

Plugging the values of f(a), f(b), a and b in the above formula, we get

`f_(avg)=(0-(-5))/(0-(-2))  = (5)/(2)`.

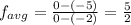Therefore, the average rate of change from x = −2 to x = 0 is
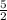`(5)/(2)`.