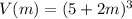INFORMATION:
We know that:
- A cube has an edge of 5 feet
- The edge is increasing at the rate of 2 feet per minute
And we must express the volume of the cube as a function of m, the number of minutes elapsed
STEP BY STEP EXPLANATION:
First, we need to use that the volume of a cube of edge e is given by:
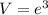
Second, we can find an expression for the variation of the edge in terms of the time. The edge starts at 5 feet, and increases at the rate of 2 feet per minute
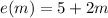
Finally, replacing the function for the edge variation in the formula for the volume of a cube
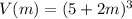
ANSWER:
The expression for the volume of the cube as a function of m is: