Question

As the distance between a satellite in a circular orbit and the central object increases, the period of the satellite .

A. increases
B. decreases
C. continuously fluctuates
D. stays the same

Answer 1

the answer is increases

Answer 2

A. increases

Step-by-step explanation:

We can answer the question by reminding Kepler's third law, which states that

"for an object in motion around a central object (such as a satellite in orbit around a planet), the cube of the distance between the satellite and the centre of the orbit is proportional to the square of its orbital period"

In formula, this can be written as

`(r^3)/(T^2)=const.`

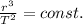
where r is the distance between the satellite and the central object while T is the orbital period of the satellite. From this relationship, we see that if r (the distance) increases, then the period of the satellite (T) increases as well.