By the polynomial remainder theorem,
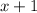
will be a factor of
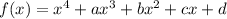
if the remainder upon division is 0, and this remainder is given by

:
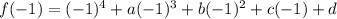
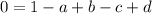
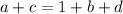
Since
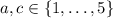
, it follows that

. But notice that if
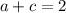
, then we have
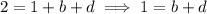
and since
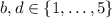
, the equation above requires that either
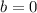
or

, which is impossible. So
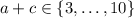
.
So we have 8 cases to check:
(1) Notice that if
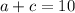
, we have
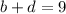
. This is only possible for
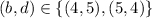
.
(2) If
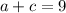
, then
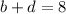
, and so we can have
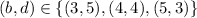
.
(3) If
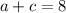
, then
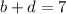
, and so

.
(4) If

, then
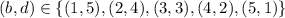
.
(5) If
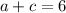
, then
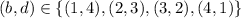
.
(6) If
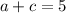
, then

.
(7) If
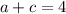
, then
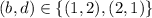
.
(8) If
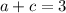
, then
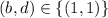
.
At the same time, we have 8 cases to consider to find how many options there are for
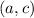
.
(1)
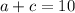
. We have only one choice of
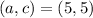
.
(2)
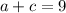
. This is the same as when
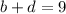
, which we found to be 2 choices.
(3) Same as
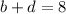
; 3 choices.
(4) Same as
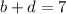
; 4 choices.
(5) 5.
(6) 4.
(7) 3.
(8) 2.
In total, there are
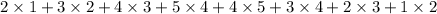
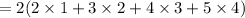
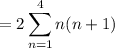

ways to choose
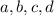
such that
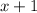
is a factor of
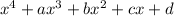
, so the answer is B.
Note the symmetry of the sum above. You can easily give a slightly briefer combinatorial argument for this answer, but I figured a more brute-force approach would be easier to follow.