Question

What is the resultant of two displacement vectors having the same direction?

a. The resultant is the sum of the two displacements having the same direction as the original vectors.
b. The resultant is the difference of the two displacements having the same direction as the original vectors.
c. The resultant is the sum of the two displacements having the direction opposite to the direction of the original vectors.
d. The resultant is the sum of the two displacements having the direction perpendicular to the direction of the original vectors.?

Answer 1

A. the resultant is the sum of the two displacements having the same direction as the original vectors

Answer 2

The correct option is a. The resultant is the sum of the two displacements having the same direction as the original vectors.

Step-by-step explanation:

I add a graph of the situation.

If we want to sum two vectors that are collinear and have the same sense, we can make that adding such as an algebraic sum.

The resultant vector will have the same direction as the originals and the same sense. Its magnitude will be the sum of the magnitudes from the original vectors.

In the graph, the vector A adding to the vector B is equal to the vector C.

If we work with its magnitudes :

`A+B=C`

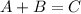
Therefore, the correct option is a.