First, we need to standardize the value 1440 and 1465 to be able to work out the z-score

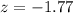
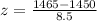
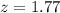
The z-scores are shown in the diagram below
To work out the probability of

we can first read on the table, the probability when
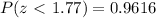
, then we subtract this value from 1, as we are interested in the area to the right of 1.77.
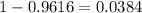
Then the area between
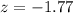
and
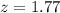
is

which is also the probability of lifespan between 1440 and 1465