Question

Ancient paintings were found on cave walls in South America. The Carbon-14 in the paintings was measured and was found to be 19% of the original weight. How old were the paintings?

Answer 1

13713.717 years

Explanation:

The exponential decay model for Carbon-14 is modeled by the following formula:

`A=A_(0)\;e^(-0.0001211\;t)`

where:

`A_0` is the initial amount of Carbon-14

A is the final amount of Carbon-14,
`A = 0.19 * A_0`

t is the elapsed time in years since the painting was made

Replacing in the formula:

`0.19 * A_0=A_(0)\;e^(-0.0001211\;t)`

`0.19=e^(-0.0001211\;t)`

`ln(0.19)=-0.0001211\;t`

`(ln(0.19))/(-0.0001211)=t`

`13713.717 years=t`

Answer 2

Painting is 13725 years old.

Explanation:

C-14 dating is the process through which age of fossils or dead tissues are determined.

One important thing about the C-14 dating is half life life period of C-14 that is 5730 years.

Now we know for C-14 decay we use the formula

`A_(t)=A_(0)e^(-kt)`

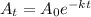
where
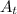`A_(t)` = present quantity of C-14

`A_(0)` = Initial quantity of C-14

k = Decay constant

t = Duration or time

We will calculate the decay constant first to use this formula for age determination further.

For Half life of C-14

A_{t}=A_{0}e^{-kt}

`(1)/(2)=1.e^(-k(5730))`

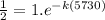
Taking ln on both the sides

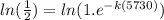
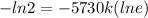
`ln((1)/(2))=ln(1.e^(-k(5730)))`

`-ln2=-5730k(lne)`

k =
`(ln2)/(5730)=(1.21)(10)^(-4)`

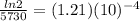
Now we have been given in the question that C-14 found to be 19% and we have to determine the age of the painting.

`A_(t)=A_(0)e^(-kt)`

`0.19=1* (e^{-(1.21* 10^(-4))t})`

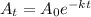
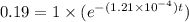
We will take ln on both the sides

`ln(0.19)=ln[1* (e^{-(1.21* 10^(-4))t})]`

`-1.6607=-(1.21* 10^(-4))t* lne`

`t=(1.6607)/(1.21* 10^(-4))`

t = 1.3725×
`10^(4)`

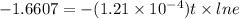
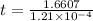
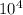
t = 13725 years

Therefore, painting is 13725 years old.