Question

Manuel wants to buy a window shade to cover the window and frame shown. The window is in the shape of a regular The radius of the window, including the frame, is 2 ft, and the measure of each edge of the octagonal frame is 1.52 frame octagon.

What is the approximate area of the window that needs to be covered, including the frame?

A. 2 ft2

b. 7 ft2

c. 11.2 ft2

d. 22.5 ft2

Answer 1

C. 11.2

Explanation:

Answer 2

Option (c) is correct.

Area of window is 11.2 ft²

Explanation:

Given : A window in shape of a regular octagon and a frame having measure of each edge length 1.52 ft.

We have to find the approximate area of the window that needs to be covered.

Consider the given octagonal window.

Since, The edge length of window is 1.52

Perimeter = 1.52 × 8 = 12.16 ft

Area of window = 8 × Area of each triangle.

Area of window =
`8* (1)/(2)\cdot apothem \cdot base`

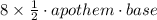
We have to apothem as,

Measure of central angle of an octagon is
`(360)/(8)=45^(\circ)`

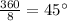
Thus, Apothem is ,

Using trigonometric ratio,

`\cos22.5^(\circ)=(a)/(2)`

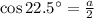
Simplify for a,

We have,

`\cos22.5^(\circ) \cdot 2=a`

Thus, Area of window is

Area of window =
`8* (1)/(2)\cdot \cos22.5^(\circ) \cdot 2 \cdot 1.52`

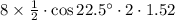
Thus, Area of window is 11.2 ft²